带“跟踪与保持”信号解调器的稳定斩波放大器
作者:Alberto Bilotti(电机及电子工程师学会终身高级会员)和 Gerardo Monreal
摘要—“跟踪与保持”(T/H) 和求平均值函数可以取代斩波放大器中传统的信号解调器。此安排无需使用低通滤波器即可实现偏移取消,忽略输入峰值产生的残余偏移。噪音分析显示,T/H 解调器可降低白噪音信噪比 (SNR),虽然使用最大占空比和最小放大器带宽可将这种降低最小化。
索引术语—宽带白噪音半导体、斩波放大器、偏移取消、跟踪与保持解调器。
I. 简介
放大器的稳定斩波是一项著名的降低输入直流 (DC) 偏移和低频输入噪音的技术,低频输入噪音通常会降低精确 DC 放大器的性能 [1]−[3]。图 1 显示基本原理。
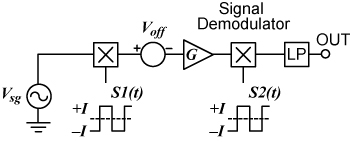
图 1. 传统的稳定斩波放大器。
输入信号首先乘以频率 ƒclk 的单位对称方波函数 S1(t),其次通过增益 G 的放大器放大,再乘以类似于 S1(t) 的开关函数 S2(t),最后进行低通滤波。第一个乘法将输入信号频谱换算成高频 (HF) 区,第二个乘法将信号解调回基带,从而恢复已放大的原始信号。另一方面,输入参考放大器 DC 偏移和低频噪音元件只通过第二个乘法流程。例如,DC 偏移转换成 HF 方波函数后,通过低通滤波器完全衰减。乘法函数通常由简单的金属氧化物半导体 (MOS) 开关组合(受 CLK 信号控制)执行。
传统斩波器的问题在于第一次乘法开关瞬态变化可能产生寄生偏移,这些偏移即使通过低通滤波器也无法取消。另一个问题为,必须使用低通滤波器来衰减偏移产生的残余方波波痕。此问题在单片斩波器中尤其严重,因为多极 LP 滤波器需要相当大的硅面积。
接下来,我们描述使用跟踪与保持 (T/H) 解调器替换传统信号解调器的优点与缺点。
II.跟踪与保持信号解调器
让我们假设稳定斩波放大器 Vsg 的输入信号是受限于奈奎斯特频率 (ƒclk ⁄ 2) 的带宽,而且放大器没有噪音。
尽可能缩小放大器的频带 [2] 或安装已将中心频率锁定到 ƒclk 的带通 (BP) 滤波器 [4],从而大幅降低输入开关瞬态峰值产生的残余偏移,该峰值持续时间比 Tclk ⁄ 2 短。如果斩波器在相对较高的频率下工作,而且输入峰值持续时间与 Tclk ⁄ 2 相比不再微不足道,为得到类似的结果,则扩大放大器的频带且使 S2(t) 开关函数低于 50% 占空比(如图 2 所示),从而在已放大的峰值所在的 Δt 间隔中输出为零。此技术引入由 Δt ⁄ (Tclk ⁄ 2) 给予的信号衰减和更大的白噪音。
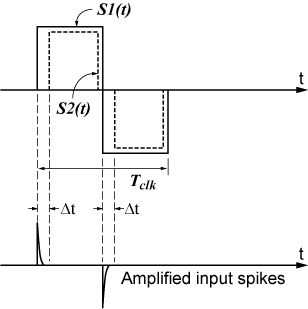
图 2. 通过第二个乘数开关函数的适当成形移除输入峰值。
当保持函数正确包含在信号解调器内时,可以避免信号衰减和放宽低通滤波器要求。例如,图 3 显示的信号解调器包含一个双 T/H 和一个加法器(或求平均值)安排,可替代图 1 的传统信号解调器。
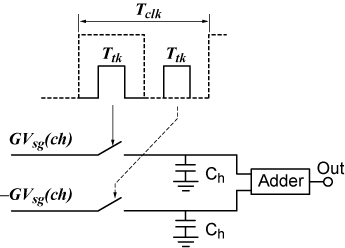
图 3. T/H 解调器。
T/H 输入是非反相和反相放大斩波信号,T/H 输出则应用于加法器。T/H 开关由在 CLK 期间产生的脉冲和带占空比 d 的 CLK_栏定时信号关闭。我们假设斩波信号通过放大器而不失真,这意味着放大器带宽是 ƒclk 的五倍或以上。
在此安排下,假设理想的开关和零偏移,以及回想在每个 CLK 半周期时的斩波信号变更记号,则每个 T/H 都恢复原始信号 G × Vsg,且加法器生成 2G × Vsg 输出(在每个 CLK 半周期更新)。
就 DC 偏移(或低频噪音元件)而言,不斩波的偏移不会更改各个 CLK 半周期的记号,因此,T/H 输出是带相反极性的 DC 电压,偏移由加法器取消。
以下概括了在稳定斩波放大器中使用此信号解调器的优点。
- 不需要任何 LP 滤波即可消除偏移。只有 T/H 不匹配和加法器不准确时才会产生残余偏移。
- 由于交错采样,与输出波形相关的典型的梯形波痕有 2ƒclk 基频,简化了移除流程。
- 如果需要,对跟踪脉冲进行适当的相对分析,没有衰减惩罚,从而消除输入开关瞬态产生的残余偏移。
最近报道了一种信号调整器,其使用带 T/H 信号解调器的斩波放大器,可消除开关式霍尔磁传感器中出现的相对较大的偏移 [5]。
图 4 显示了使用之前描述的 T/H 信号解调器的全差分斩波器。方波 5-V 时钟信号 CLK1 驱动的开关 SWi 执行第一个乘法,采样脉冲 CLK2 和 CLK3 驱动的 SW1 和 SW2 以及 C1、C2、平均电阻 R1 和 R2 组成 T/H 信号解调器。由放大器输出馈电的带相反极性的类似 T/H 解调器已包含在内,以生成全差分输出。T/H 开关是补充的 MOS (CMOS) 传输晶体管,输入开关是简单的 N-通道传输晶体管,旨在提高输入瞬态峰值的振幅。理想的放大器是 40× 增益和 3 MHz 的 3-dB 带宽,使用输入 DC 发生器 Voff 模拟其偏移。图 4 还显示 CLK 波形、采样脉冲 CLK2 和 CLK3 大约在 CLK1 半周期的中心出现。
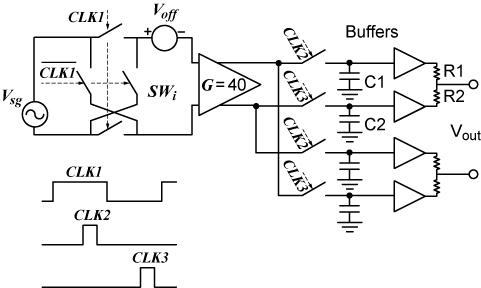
图 4. 使用 T/H 信号解调器的全差分斩波器。
对图 4 的电路执行 SPICE 模拟时,使用 ƒclk = 160 kHz、d = Ttk ⁄ Tclk = 0.25,0.5-mV 振幅的 5-kHz 正弦输入信号和 5 mV 的 DC 输入偏移。所有装置的 SPICE 模型参数从标准 2-µ 混合双极 CMOS (BiCMOS) 流程中衍生出来。
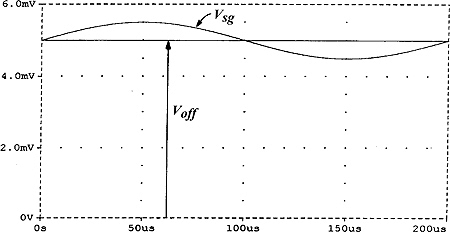
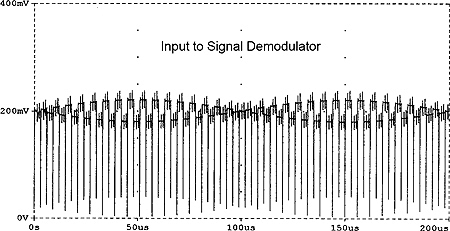
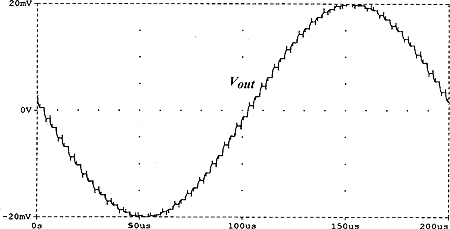
图 5(a) 显示输入信号和放大器 DC 偏移波形,图 5(b) 显示在 T/H 解调器之前放大器输出的电压波形。尽管斩波信号似乎嵌入到相对较大的瞬态脉冲中,但是通过对采样脉冲进行适当的相对分析,可以完全恢复原始信号波形,如图 5(c) 的输出电压波形所示。
(a)
(b)
(c)
图 5. 图 4(a) 输入信号和输入 DC 偏移中斩波器的 SPICE 模拟。(b) 在 T/H 解调器之前的放大器输出电压波形。(c) 输出电压。
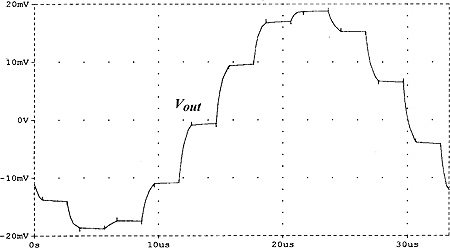
输出电压就是放大后的输入信号,除采样保持 (S/H) 函数特有的类似波痕外。就像在所有采样数据系统中一样,随着信号频率接近奈奎斯特频率 ƒclk ⁄ 2,残余梯形波痕就越相关,可能需要后斩波 LP 滤波器才能恢复未失真的波形。例如,图 6(a) 显示了和图 5(c) 相同的输出波形,但是斩波器的信号频率为 30 kHz,例如在 ≈ 0.4(ƒclk ⁄ 2) 时,由于过度的梯形波痕,输出波形看上去严重失真。图 6(b) 显示如何使用 60khz 的 −3-dB 频率的后斩波器单极 LP 滤波器适当恢复原始波形。
(a)
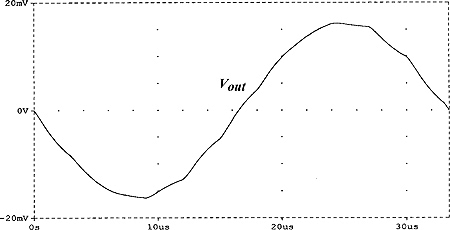
(b)
图 6. 类似于图 5(c) 的输出波形,但是使用图 4 的斩波放大器,以 ƒsg = 30 kHz 工作。(a) 没有任何 LP 滤波。(b) 带 60khz 的 −3-dB 频率的后斩波器单极 LP 滤波器。
III.输入参考偏移
在实际电路中,偏移取消主要受限于解调器不匹配。如果 Voia 是放大器输入参考偏移,图 4 的加法器中电阻 R1 和 R2 之间的任何相对不匹配 M = ΔR ⁄ R 将在斩波器中生成输入参考偏移 M × Voia,而 T/H 解调器产生的等量偏移 Vob 和缓冲不平衡将生成输入参考偏移 Vob ⁄ G。假设输入峰值产生的残余偏移已消除,而且所有不平衡和偏移是带高斯分布和零均值的统计独立的随机函数,我们可以为斩波器输入参考偏移 Voich 编写
(1)
其中 σ(x) 是 x 和 G 放大器增益的标准偏差。
表达式 (1) 显示,根据解调器不平衡和放大器输入参考偏移,过度提高放大器增益不会有太大改变。
正如在传统斩波器中一样,放大器 DC 传输特性中的不对称性也会在非反相和反相放大斩波信号中引入偏差,使偏移取消受到限制。一般而言,与 (1) 中描述的方法相比,使用匹配的差分放大器可以忽略这种错误。
此外,添加保持函数和使用带宽比时钟频率大得多的放大器,可以降低此类解调器的信噪比 (SNR),如下一节所示。
IV.噪音问题
在所有实际案例中,放大器输入参考白噪音电压产生的白噪音电压会放大 G 倍且受限于放大器带宽,如图 2 解调器的各个 S/H 的输入端所示。
让我们首先分析一个简单 T/H 的白噪音行为。假设在带宽 BWn 的理想矩形噪音频谱和功率频谱密度 ηi 下,应用白噪音电压至 T/H 的输入端并在 T/H 输出端调用 ηo 噪音功率频谱密度。正如之前所述,为避免斩波信号失真,放大器带宽必须远远大于 ƒclk,因此 T/H 开关对 BWn » ƒclk 和噪音抽样不足。
长度 d × Tclk 的跟踪脉冲生成的噪音不会大幅增加输出噪音,但是在保留期间 (1 − d)Tclk 额外噪音会被引入,因为围绕时钟频率谐波调整的所有高频 (HF) 噪音元件折叠到基带中,形成 ηo > ηi。出现这些混淆现象是因为周期性的保持相当于等值的理想 S/H 函数,每当输入频谱超过奈奎斯特频带时,就会出现明显的混淆 [6]−[8]。
费舍尔已分析了理想 T/H 的白噪音传输函数 [6],假设输出噪音功率谱密度等于跟踪间隔期间生成的噪音功率与保持间隔期间生成的噪音功率之和。让我们着重关注范围 0 < ƒ < ƒclk ⁄ 2 和回想 [6] 的表达式 A2、B5a 和 B5b,我们可以为简单 T/H 的噪音功率谱密度传输函数编写一条通用表达式:
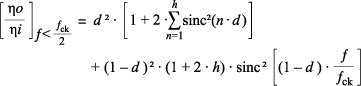
(2)
其中第一项和第二项分别代表跟踪与保持贡献,ηi 和 ηo 分别是输入和输出噪音谱功率密度和
d 占空比 (Ttk ⁄ Tclk);
ƒclk 1 ⁄ Tclk = 时钟频率;
h 是 BWn ⁄ ƒclk比最接近的整数;
sinc(x) [sin(π × x) ] ⁄ π × x。
注意,当 d = 0 时,存在纯 S/H 函数且 ηo ⁄ ηi = (1 + 2 × h) × sinc²(ƒ ⁄ ƒclk),当 d = 1 时,不存在 S/H,跟踪开关永远为开且 ηo ⁄ ηi = 1。当参数 h 为零时,不存在混淆,因为噪音输入频谱始终低于 ƒclk ⁄ 2。当 h = 1、2、3等时,存在额外噪音,因为输入噪音频谱超过 ƒclk ⁄ 2,达到第一、第二、第三 CLK 谐波等,并折回到奈奎斯特频带。因为输出噪音频谱在奈奎斯特频带内近似于平坦,可以简化 (2),假设在最坏的情况下,恒定功率谱密度等于当ƒ = 0 时出现的最大值。因此
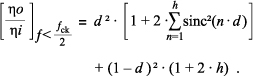
(3)
表达式 (3),在给定奈奎斯特频带中适用于简单 T/H 函数的白噪音降低下,取值范围为 0 < d < 1 时,按不同的 h 值在图 7 中进行标绘。正如预期一样,当 d = 0 时噪音降低最大,并随着 h 增加而增加。
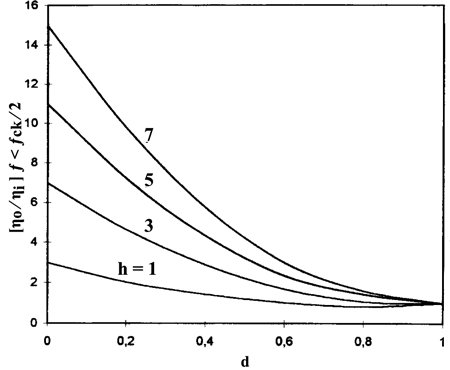
图 7. 针对 ƒ < ƒclk ⁄ 2 的简单 T/H 的白噪音功率谱密度传输函数,其中 d 是跟踪脉冲占空比,h 是 BWn ⁄ ƒclk 最接近的整数,且假设在 ƒ = 0 时出现最坏情况。
返回到图 3 的解调器,添加了两个 T/H 的噪音输出,两个噪音输出都由相同的噪音电压馈电,但是极性相反。对于频率远远低于 ƒclk 的噪音输入频谱的低频区,T/H 输出噪音电压相互关联,因此互相抵销。此取消操作包含 DC 偏移电压和相对低频 1 ⁄ ƒ 噪音。对于其他高达 BWn 的输入噪音频谱,大部分噪音电压互不关联,他们的功率谱密度由加法器直接计算总数。
因此,根据最初的假设 BWn » ƒclk,我们可以假定在两个 T/H 输出端生成的白噪音电压是混淆现象造成的,因此互不关联;图 3 的解调器显示最坏情况下的输出噪音功率谱密度 ≈ 2ηo。因为输出信号功率是输入信号功率的四倍,所以解调器噪音因素 (NF) 成为(只要与白噪音相关)
(4)
其中 η o⁄ ηi 指适用于 ƒ < ƒclk ⁄ 2 的简单 T/H 的噪音功率谱密度传输函数(图 7)。
例如,对于 d = 0.3 和 h = 5,图 7 的 η o⁄ ηi 比率是六,信号解调器的噪音因素是三。由于跟踪脉冲宽度不能高于时钟 1 半周期,允许的最大占空比是 0.5,图 7 显示混淆现象产生的噪音是引起 T/H 解调器噪音的主要因素。
V. 总结
本文描述了斩波稳定放大器的性能,其中信号解调或第二个乘法函数由双 T/H 和加法器安排执行。与传统斩波器相比,此方法最重要的优点是取消放大器输入偏移、低频输入噪音元件和输入开关峰值产生的残余偏移,不需要任何低通滤波。可实现的最大偏移取消受 T/H 不匹配和加法器准确性限制。
为避免输出波形出现过度的梯形波痕,输入信号频谱带宽最好比奈奎斯特频率小 0.2 倍。否则,可能需要后斩波 LP 滤波器。
最后,这些解调器显示保持函数降低了白噪音;此降低在允许的最大占空比 0.5 和最小放大器带宽时为最小。
鸣谢
作者在此感谢 Electrónica Bilotti 的 D. Barrettino 提供建议。
参考文献
[1] K. Hsieh et al., "A low-noise chopper stabilized differential switched-capacitor filtering technique," IEEE J. Solid-State Circuits, vol. SC-16, no. 6, pp.708-715, Dec. 1981.
[2] C. C. Enz et al., "A CMOS chopper amplifier," IEEE J. Solid-State Circuits, vol. SC-22, pp.335-341, June 1987.
[3] C. C. Enz and G. C. Temes, "Circuit techniques for reducing the effects of op-amp imperfections:Autozeroing, correlated double sampling, and chopper stabilization," Proc.IEEE, vol. 84, pp.1584-1613, Nov. 1996.
[4] C. Menolfi and Q. Huang, "A low-noise CMOS instrumentation amplifier for thermoelectric infrared detectors," IEEE J. Solid-State Circuits, vol. 32, pp.968-976, July 1997.
[5] A. Bilotti et al., "Monolithic magnetic hall sensor using dynamic quadrature offset cancellation," IEEE J. Solid-State Circuits, vol. 32, pp.829-836, June 1997.
[6] J. S. Fischer, "Noise sources and calculation techniques for switched capacitor filters," IEEE J. Solid-State Circuits, vol. SC-17, pp.742-752, Aug. 1982.
[7] C. Gobet, "Spectral distribution of a sampled first order lowpass filtered white noise," Electron.Lett., vol. 17, no. 19, pp.720-721, Sept. 1981.
[8] C. Gobet and A. Knob, "Noise analysis of switched capacitor networks," IEEE Trans.Circuits Syst., vol. CAS-30, pp.37-43, Jan. 1983.
1997 年 11 月 10 日收到原稿;1998 年 5 月 2 日修订。此作品由 Allegro™ MicroSystems 公司提供支持。此论文获副主编 M. Biey 推荐。
A. Bilotti 携手 Electrónica Bilotti, Olivos 1636,阿根廷。
G. Monreal 携手 Sensor Development Group, Allegro MicroSystems, LLC, Concord, NH 03306 美国。
出版商项目标识符 S 1057-7122(99)02748-8。
本文描述的信号解调器已整合到 A3150、A3210、A3240、A3260、A3280、A3361 和 A3515 霍尔效应传感器 IC。本文最早刊登于 IEEE Transactions on Circuits and Systems, I:Fundamental Theory and Applications, Vol. 46, No. 4, April 1999。重印获得许可。
1057-7122/99$10.00 © 1999, IEEE